The case against the fluffy metrics (Part 2) - Power

Introduction

So, a few weeks ago I wrote a blog post in which I described metrics, like power and rate of force development, as fluffy metrics. And you may have wondered "...what on earth is he on about...?" 

I'm glad you asked this because I want to provide a little bit more context to my comments on power (I’ll address RFD in another post).

Anyone who has ever read anything I've written, listened to any webinars I've been on, or watched any talks I've given will know that I'm a big proponent of impulse as a 'main player' force-based metric. In fact, so important is impulse that it could be described as an outcome, driver, or strategy metric depending on the context in which you report it.

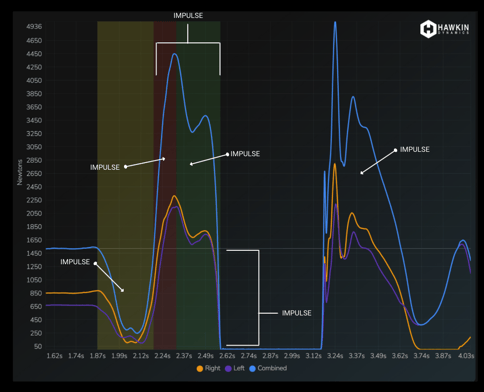
A picture of various impulses achieved during the CMJ. These are just a few, there is more that can be calculated. The one that we care about the most is under the blue curve and in the green shaded region above system weight (grey line running horizontally). Impulse is simply an area, force * time for a specific area.

RE Impulse:

And, of course, when you couple this with my use of what could be considered a derogatory term (fluffy), it might seem that I have a bee in my bonnet about these metrics. I promise you, that really isn't the case. In fact my PhD was on power in resistance exercise. With that in mind, I think I have a pretty decent understanding of it, and it definitely has a place in force-time analysis. However, it requires context.

So, with that in mind, and before we go on any further, let's make sure that we're all on the same page with what power actually is.

Power

So, (mechanical) power describes the rate at which work is performed. Pretty simple. Okay, so what is work? Easy, work describes the product of force and displacement. That's right, if you have a method that enables you to measure how hard you push (or pull) something and how far it moves while you're pushing or pulling it then you can calculate the work you've performed. Of course, the many different force plate measurement systems that are out there let us not only record force and displacement, but because they also give us movement duration(s) we can also calculate power.

S&C biomechanics and the wonderful research of John Garhammer...

If we want to dig a little deeper then we should understand that work is proportional to the change in (mechanical) energy, typically both potential and kinetic energy, and any one who is interested in how this can be applied to lifting should get stuck into the awesome research of Dr. John Garhammer (he provides a great summary here). Fascinated by the human's capacity to perform work and generate power, he studied Olympic weightlifting, focusing his research on the second pull. By improving on the way that these movements were studied he discovered that weightlifters performed huge amounts of work and they performed it blooming quickly. So, it’s safe to say that weightlifters are real powerhouses! 

Honestly, if you're interested in this kind of thing, and why wouldn't you be, then dig out his first few studies (this one in particular). 

The key thing to take from Garhammer’s work is that at no point (and please correct me if I'm wrong) did he consider peak power. And why would he? He was interested in the work performed during the different phases of the snatch and clean, focusing predominantly on the second pull. And, you see, this is really important because peak power, i.e. the power achieved by performing work over a fraction of a second didn't matter. Why would it? It's worth bearing in mind that Garhammer used motion analysis techniques, studying these movements across multiple 0.04 s intervals (filming at a frame rate of 25 frames per second). 

That means that had Garhammer reported peak power then he would have been reporting the rate at which work was performed during a 40 ms period. Apply this logic to force plate assessment and if you’re recording force at 1000 samples per second (Hz), peak power will give you the rate of work performed over 1 millisecond. (*video of this below)

With the above in mind, as yourself: why might the power achieved over a fraction of a second be of interest? What rationale could we provide to support this?

If we have one then use it. If not, don't. It's as simple as that.

Okay, it’s worth reminding ourselves that the power that Garhammer reported was what we often refer to as mean power. So, if we don’t have a rationale for considering peak power (and you might have of course), could (and should) we study mean power instead?

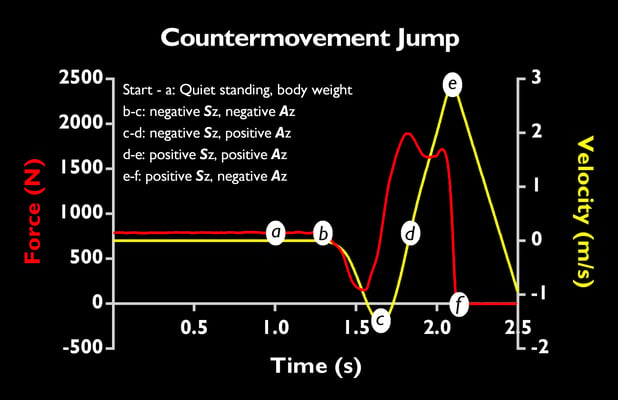
If you have a good rationale for studying it then go for it. If not, don't. Remember, you must take total ownership of your data for it to be truly useful to you. However, I’m going to try and explain its limitations in the next section using the countermovement jump (CMJ) as an example.

Video on how to find peak power from a force plate operating at 1000Hz.

Practically applying power to common force plate assessments

So, what does the power metric tell us about lower-body power? You might think that this is a really silly question. However, unless we understand this there’s really no point in studying it (remember, own your data).

You see, in this kind of scenario power could be considered an outcome metric and to understand it fully (and I really think this is important) we’d have to delve into other metrics. Because power is the rate at which work is performed, surely the range of motion that this work is performed over must be considered? It’s part of the puzzle after all.

Let’s consider two CMJs, where the same jumper achieved 54 cm in the first jump at a body weight of 926 N and 44 cm during the second jump at a body weight of 1000 N.

The 54 cm jump at a body weight of 926 N

In the first jump, the jumper dips 41 cm. He has to reverse this during the propulsion phase, adding another 11 cm as he rises onto his toes immediately before take-off. He covers 52 cm during the propulsion phase. He does this by applying an average force of 1772 N, meaning he performs just over 921 joules of work.

He does this over 0.28 s (just over a quarter of a second), meaning that he achieves around 3,290 watts of power during the propulsion phase. Nice!

The 44 cm jump at a body weight of 1000 N

In this jump the propulsion range of motion is 37 cm (dip = 25 cm, rise to tip toe = 12 cm) and this is driven by an average force of 2354 N. So, he performs 871 joules of work. However, he does this faster than the first jump, over 0.22 s, so he achieves 3959 watts of power. Therefore, he achieves  17% more power but jumps 10 cm less? Interesting, right? I will say at this point, if this doesn’t ring any alarm bells then you really should step away from this metric. Now.

Of course, he’s heavier during the second jump. We could normalize power relative to body mass. In the first jump his relative propulsion power is 35 W/kg and in the second jump it is 39 W/kg. Well, bugger, that didn’t help us get to the bottom of these differences did it.

The second jump is more powerful, even relative to his body mass, but he still jumps 10 cm less. This is why it is so important that we avoid questions like ‘what one metric would you use?’ because they sell both you and your athletes short.

So, what’s my take-home point here? I think that it would be far healthier for S&C to consider power as an outcome metric. A consequence of movement. Can it be important? Of course. However, we typically want to know how quickly athletes can move. So let’s study their velocity. Wanting to avoid the 1-metric nonsense though, I recommend considering the following (although you can use any combination of metrics just as long as you critically review whatever rationale you have for using them):

• Jump height and/or mean power/mean velocity

• Mean net force (force less body weight), perhaps from the braking and propulsion phase

• Braking and propulsion phase duration

• Down and up phase range of motion

I would argue that what these metrics can’t tell you probably isn’t going to be that important, typically at least. As always though, critically evaluate the tests you choose, the protocol you use, and the metrics you’ll study. Own as much of the athlete assessment process as possible.

So, is power bad? No. Is it the one-stop athlete assessment metric that it’s often thought to be. Also: No! Don’t sell yourselves or your athletes short – open your mind to all of the other fascinating, useful metrics that are out there in the force plate world.