How we Calculate Jump Height from Take-Off Velocity

INTRODUCTION

When performing a vertical jump, the athlete leaves the ground at a given vertical velocity. The instant at which they leave the ground is commonly termed the instant of take-off. The precise vertical velocity at take-off (termed take-off velocity herein) attained depends on the magnitude of the net impulse generated during the propulsive phase (i.e., when extending ankles, knees, and hips) of the jump. In other words, a larger net impulse applied to the athlete’s center of mass (COM) during the propulsive phase will lead to a greater take-off velocity (1). After take-off, the athlete’s COM continues to follow an upward vertical trajectory, but they are subjected to a constant downward acceleration due to gravity. Gravitational acceleration is almost always equal to -9.81 m·s^-2 (the negative sign denotes the downward direction) and it acts to decelerate the athlete from the instant of take-off. Thus, the athlete’s velocity begins to reduce from the very moment they leave the ground until they reach a momentary velocity of 0 m·s^-1 (2). In other words, the athlete stops momentarily whilst in the air and this coincides with the instant at which they achieve maximum COM height (i.e., the peak COM position during the jump). The athlete then begins to descend towards the ground under the same constant gravitational acceleration. Thus, the athlete’s velocity begins to increase (in the downward direction) as they accelerate towards the ground until the moment they contact it. The instant at which they contact the ground is commonly termed the instant of touchdown and the touchdown velocity is almost identical to the take-off velocity. I say almost identical because differences in the athlete’s joint geometry between take-off and touchdown will lead to differences in their COM position at each of these two instants and the corresponding velocity. Between the instants of take-off and touchdown, the athlete can be considered a projectile in free flight, with gravity being the only force that influences their motion (based on the assumption that air resistance is negligible). Because of this, the jump height attained depends entirely on the take-off velocity (e.g., a greater take-off velocity results in a higher jump). This statement holds true irrespective of the athlete’s body mass for reasons explained in detail later in this article.

Jump height is the key performance indicator of vertical jumping ability and so it is usually the primary variable of interest for those who conduct vertical jump testing. As mentioned earlier, the jump height attained depends entirely on take-off velocity so if we know an athlete’s take-off velocity, we can calculate their jump height. We can do this via the application of either the relevant equation for one-dimensional motion or the equations that explain the conservation of mechanical energy principle (3). Performing vertical jump tests on a force plate is becoming increasingly common in sport owing to advances in force plate technology like ours (4). The primary outcome variable of interest is usually jump height, irrespective of the sport. With a rise in the number of jump test trials being conducted globally (2.1 million no less by our users in 2023 alone) comes a requirement for accompanying education around the biomechanics of vertical jumping. Such education should, in my opinion, include improving sports practitioners’ understanding of how key variables of interest (e.g., jump height) are calculated using simple language and clear equations to explain the involved mathematical processes. Therefore, this article aims to explain the equations for calculating jump height based on the COM take-off velocity. The equations are deconstructed and explained in plain language. I hope you find it useful.

CALCULATING JUMP HEIGHT FROM TAKE-OFF VELOCITY

As mentioned above, when we know the take-off velocity alone for a given jump, we can estimate the jump height by applying either the relevant equation for one-dimensional motion or the equations that explain the conservation of the mechanical energy principle. Both approaches are discussed in detail below. Remember, each approach assumes that air resistance is negligible and so the athlete’s mass is only subjected to a constant gravitational acceleration, equal to -9.81 m·s^-2, during the flight phase of the jump and no other external forces. Let’s say, in the following examples, the athlete’s take-off velocity during any given vertical jump test was 2.45 m·s^-1, and this was derived from a validated (5) Hawkin Dynamics force plate (Figure 1).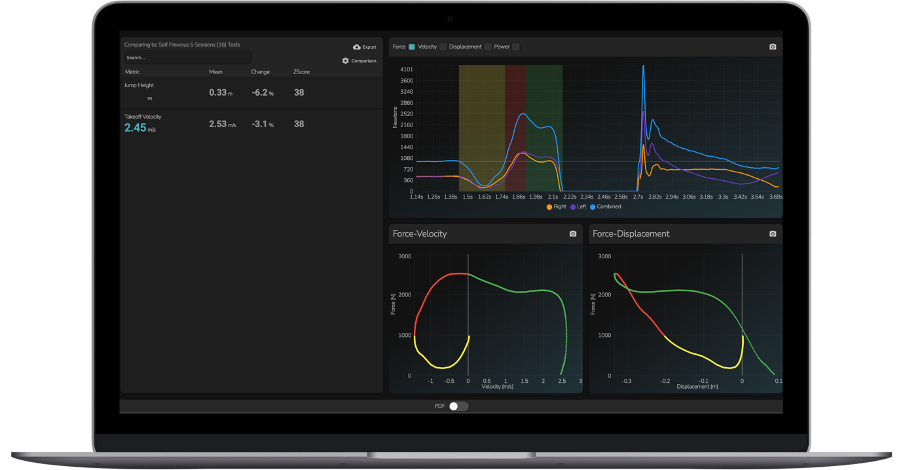

Figure 1: The center of mass force-time record (top right), force-velocity record (bottom-middle), and force-displacement record (bottom-right) for a countermovement jump. The athlete’s take-off velocity (2.45 m·s^-1) is shown (top-left) but the corresponding jump height is hidden.

APPLY THE EQUATION FOR ONE-DIMENSIONAL MOTION

Based on the equations for one-dimensional motion, we know that the displacement (i.e., the change in position) between some initial and final instant is equal to the average velocity between the same initial and final instants multiplied by the change in time between the same initial and final instants. This can be expressed in the following equation, where Δs is displacement, 𝑣̅ is average velocity and Δt is change in time:

∆𝑠 =  𝑣̅ × ∆𝑡

Before we proceed, our initial and final instants of interest need to be defined. Well, jump height can be defined as the peak vertical displacement of the athlete’s COM following the instant of take-off, so we let take-off be the initial instant and peak vertical displacement be the final instant of interest.

We know the athlete’s take-off velocity, but this is different from the average velocity between take-off and the peak vertical displacement (i.e., the information we need to know for the above formula). To calculate average velocity, we first need to calculate the athlete’s change in velocity between take-off and peak vertical displacement. To do this, we simply subtract the velocity at the instant of peak vertical displacement from take-off velocity. This can be expressed in the following equation, where Δv is change in velocity, v_peak is velocity at the instant of peak vertical displacement and v_to is take-off velocity:

∆𝑣 = 𝑣_{𝑝𝑒𝑎𝑘} − 𝑣_𝑡𝑜

We know that the velocity at the instant of peak vertical displacement will always be 0 m·s^-1 because this reflects the transition point from the upward to downward acceleration (i.e., the momentary pause when the maximum jump height is achieved). Thus, the equation above can instead be expressed as follows:

∆𝑣 = 0 − 𝑣_𝑡𝑜

Alternatively, the zero can be removed from the above equation along with the minus sign to give us the absolute value of take-off velocity and presented as follows:

∆𝑣 = 𝑣_𝑡𝑜

Therefore, we only need to know what the take-off velocity is to determine the change in velocity between the instants of take-off and peak vertical displacement.

For example, for the athlete whose take-off velocity is 2.45 m·s^-1, we would calculate the change in velocity as follows (I know this is obvious, but I want to explain each step of the process):

∆𝑣 = 0 − 2.45

So:

∆𝑣 = 2.45 m·s^-1

The next step is to calculate the average velocity by dividing take-off velocity by two. Remember, we calculate the average (mean) by adding numbers together and then dividing by the total number of numbers. Although two numbers for velocity are involved in this calculation (i.e., velocity at peak vertical displacement and take-off), we do not need to bother adding velocity at peak vertical displacement to take-off velocity because the value of the former is 0 m·s^-1. Thus, the equation for calculating average velocity between take-off and peak vertical displacement can be presented as follows:

𝑣̅ = 𝑣_𝑡𝑜 / 2

When applied to the present example of the athlete whose take-off velocity is 2.45 m·s^-1, average velocity can be calculated as follows:

𝑣̅= 2.452 /2

So:

𝑣̅= 1.23 m·s^-1

So, as seen above, we have calculated the athlete’s average velocity take-off and peak vertical displacement but that only provides us with part of the information required to calculate the height jumped. The next job is to calculate the time between take-off and peak vertical displacement. Unfortunately, we do not have any time measure at all in this example. Luckily, though, we know that change in time is equal to change in velocity divided by acceleration (remember, gravitational acceleration during the flight phase is equal to -9.81 m·s², but we use the absolute value in our calculations). This can be expressed in equation form as follows, where g is gravitational acceleration:

∆𝑡 = ∆𝑣 / 𝑔

So:

∆𝑡 = 𝑣_𝑡𝑜 / 𝑔

So:

∆𝑡 = 2.45 / 9.81

So:

∆𝑡 = 0.25 s

Finally, we can go back to the first equation presented in this section to calculate the peak vertical displacement (i.e., the peak vertical displacement of the COM relative to take-off [i.e., jump height]) by multiplying average velocity by change in time.

∆𝑠 = 𝑣̅ × ∆𝑡

So:

∆𝑠 = 1.23 × 0.25

So:

∆𝑠 = 0.31 m

In other words, the athlete’s jump height was 0.31 m based on a take-off velocity of 2.45 m·s^-1 (Figure 2).

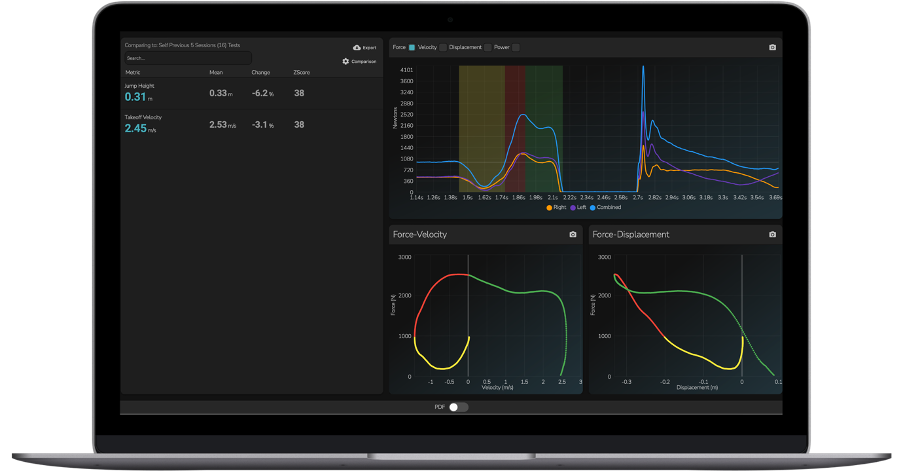
Figure 2: The center of mass force-time record (top right), force-velocity record (bottom-middle), force-displacement record (bottom-right) for a countermovement jump. The athlete’s take-off velocity (2.45 m·s^-1) is shown (top-left) and now also is the corresponding jump height of 0.31 m (also top-left).

The above description provided a step-by-step approach to calculating jump height from take-off velocity based on the equations for one-dimensional motion, but the formula can be simplified to the following (as is often reported in journal articles):

∆𝑠 = 𝑣̅ × ∆𝑡

So:

∆𝑠 = (𝑣_𝑡𝑜 / 2) × (𝑣_𝑡𝑜 / 𝑔)

So:

∆𝑠 = 𝑣_𝑡𝑜² / 2𝑔

Going back to the original example of an athlete who achieved a take-off velocity of 2.45 m·s^-1, we can check that this simplified formula gives us the same answer as earlier:

∆𝑠 = 2.45² / (2 × 9.81)

So:

∆𝑠 = 6.00 / 19.62

So:

∆𝑠 = 0.31 m

APPLYING THE CONSERVATION OF MECHANICAL ENERGY PRINCIPLE

Based on an understanding of the conservation of mechanical energy principle, we know that kinetic energy produced during the propulsive phase of a jump is equal to the potential energy at the apex of the jump (i.e., when peak vertical COM displacement is achieved). The equations for kinetic energy and potential energy are as follows:

kinetic energy = potential energy

So:

(𝑚 × 𝑣_𝑡𝑜²) / 2 = 𝑚𝑔ℎ

Where 𝑚 = mass, 𝑣_𝑡𝑜 = take-off velocity, 𝑔 = gravitational acceleration and ℎ = center of mass height

Because body mass features on both sides of the equation and it is constant during the jump, it can be removed from each side (which is why it doesn’t influence the calculation) and expressed thusly: (𝑣_𝑡𝑜² / 2) = 𝑔ℎ

Let’s say, in line with the above example, that the athlete’s take-off velocity is 2.45 m·s-1 to enable us to deduce the following so far:

(2.45² / 2) = 9.81 × ℎ

We need to get ℎ on its own, so we rearrange the equation by placing g on the other side of the equals sign like so:

(2.45² / 2) ÷ 9.81 = ℎ

Or, for better presentation, like so:

(2.45² / 2) × (1 / 9.81) = ℎ

Which can be simplified to the following:

2.45² / (2 × 9.81) = ℎ

Or, without the numbers, it may be presented like this:

𝑣_𝑡𝑜² / 2𝑔 = ℎ

Therefore, the answer to the question is as follows:

2.45² / (2 × 9.81) = ℎ

So:

6.00 / 19.62 = ℎ

So:

ℎ = 0.31 m

Notice how the conservation of mechanical energy approach gives the same answer as the application of the equations of one-dimensional motion because the same simplified expression of the respective formula is applied to the information we know (e.g., the athlete’s take-off velocity and gravitational acceleration).

CONCLUSION

Our system calculates jump height from take-off velocity in a fraction of a second (along with all other metrics we report) for the countermovement jump, squat jump, countermovement jump-rebound, and drop jump. We calculate jump height from flight time for multi-rebound jumps, as is common practice for these jump types, so I’ll follow up this article with one that explains the equations for calculating jump height based on flight time in a simplistic way and explains the key factors to consider with this approach. We think it’s super important to be transparent with our calculations, so I hope that you now know (if you haven’t already!) how and why we calculate the number one metric reported in our system. Thanks for reading this post and be sure to check out our metric database and countermovement jump and squat jump playbooks for more information on what we calculate, how we do it, and why it can be helpful.

REFERENCES

1. Kirby T.J. et al. (2011). Relative net vertical impulse determines jumping performance. J Appl Biomech 27: 207-214, 2011.

2. McMahon J.J. (2018). Understanding the key phases of the countermovement jump force-time curve. Strength Cond J 40: 96-106, 2018.

3. Linthorne N.P. (2001). Analysis of standing vertical jumps using a force platform. Am J Phys 69: 1198-1204.

4. Weldon A. et al. (2021). Contemporary practices of strength and conditioning coaches in professional soccer. Biol Sport 38: 377-390.

5. Badby, A.J. et al. (2023). The Validity of Hawkin Dynamics Wireless Dual Force Plates for Measuring Countermovement Jump and Drop Jump Variables. Sensors, 23, 4820.